You can choose out of a number of predefined motion profiles in the Motion Profile Wizard.
| • | Flat |
| • | Ramp |
| • | Sine |
The flat profile is a zero order profile. It has a constant position, zero velocity and acceleration.
The ramp profile is a first order profile. It has a constant velocity and acceleration peaks at the start and end of the motion.
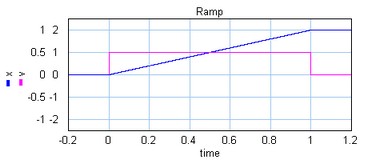
The ramp profile.
The trapezoidal profile is a second order profile. It has a constant acceleration at the start of the motion and a constant deceleration at the end of the motion.
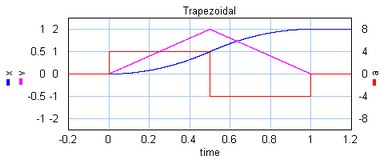
The trapezoidal profile.
This profile is most widely used in early servo systems. Because of the discontinuity in the acceleration this motion profile can still induce a lot of vibrations. Therefore in modern servo systems third order profiles are preferred.
The partial trapezoidal profile is a second order profile. It has is equal to the trapezoidal motion, but has a constant velocity part, during a fraction CV (%) of the motion.
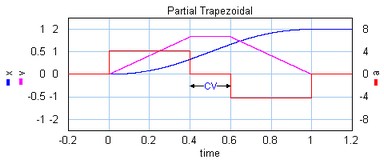
The partial trapezoidal profile.
A Geneva mechanism is an old motion profile generation mechanism. A continuously rotating crankshaft (a) generates an intermittent motion of a second shaft (b). The result is a second order profile.

A Geneva mechanism.
The motion profile generator yields the motion of the second shaft (b). It is shown below:
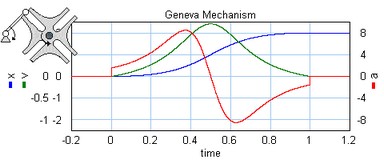
The Geneva mechanism profile.
The sine profile is a second order profile of which the displacement can be described as:
x = 0.5 - cos (p * t) / 2.
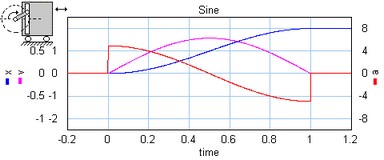
The sine profile.
The cubic profile is a third order profile of which the acceleration is constantly increasing and decreasing.

The cubic profile.
The partial cubic profile (3rd order) is a modified cubic profile with a constant velocity during a fraction CV (%) of the motion and a constant acceleration during a fraction CA (%) of the motion.
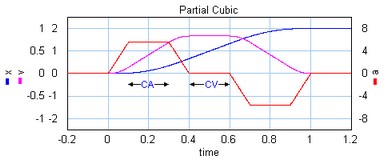
The partial cubic profile.
The cycloidal profile is a third order profile, of which the velocity can be described as:
v = stroke*(1-cos(t*a))
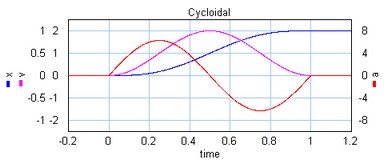
The cycloidal profile.
The modified sine profile is also a third order profile. It is a modification of the cycloidal profile to get a lower maximum velocity and a lower maximum acceleration.
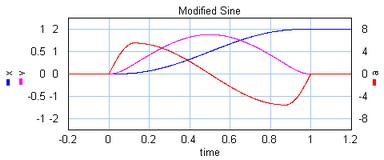
The modified sine profile.
The modified trapezoidal profile is a modification of the trapezoidal profile (to make it a third order profile). This profile yields a very low maximum acceleration.
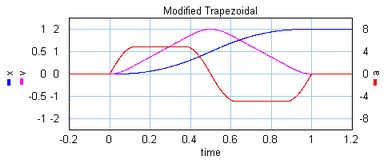
The modified trapezoidal profile.
The modified sine with constant velocity profile (3rd order) is a modification of the modified sine profile. It has a constant velocity during 50% of the motion.
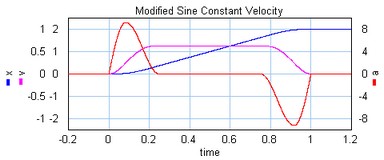
The modified sine with constant velocity profile.
General Modified Sine with Constant Velocity (MSC%)
The modified sine with constant velocity profile (3rd order) is a modification of the modified sine profile. It has a constant velocity during a user definable part of the of the motion. The non-zero acceleration part is defined by two parameters which are both defined as a fraction of the motion. The first parameters alpha (%) defines the start of the acceleration and the second parameters n (%) defines the end of the acceleration.
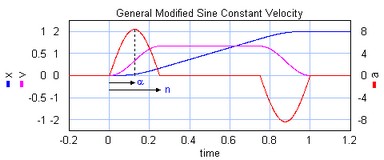
The general modified sine with constant velocity profile.
The is a third profile described by a 5th order polynomial.
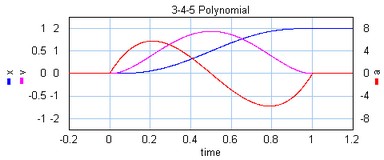
The 1-3-5 polynomial profile.
The is a third/fourth order profile described by a 9th order polynomial. The profile is characterized by two parameters that denote the initial jerk, BB, and the crossover jerk, BM. If BB is chosen zero, this a a fourth order profile. If BB is chosen non-zero, this is a third order profile.

The 1-3-5-7-9 polynomial profile.
To keep the polynomial consistent, i.e. the polynomial does not change when the amplitude is changed, the initial jerk (BB) and the crossover jerk (BM) are defined for a standard motion with:
| • | stroke = 1 |
| • | start_time = 0 |
| • | stop_time = 1 |
The specific shape of a motion profile can have a significant influence on the dynamic behavior. Some profiles minimize the maximum velocity, some profile minimize acceleration, while other profiles tend to make a tradeoff between the maximum velocity and acceleration. If we take a standard motion with stroke 1 and motion time 1 sec., the following table can be generated:
profile |
order |
vmax |
amax |
j(0) |
j(1/2) |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
infinite |
infinite |
0 |
|
2 |
2 |
4 |
infinite |
-infinite |
|
2 |
1.67 |
4.17 |
infinite |
0 |
|
2 |
2.41 |
8.49 |
infinite |
-118.5 |
|
2 |
1.57 |
4.93 |
infinite |
-15.5 |
|
3 |
2 |
4 |
32 |
-32 |
|
3 |
1.67 |
5.55 |
55.6 |
0 |
|
3 |
2 |
6.28 |
39.5 |
-39.5 |
|
3 |
1.76 |
5.53 |
69.4 |
-23.2 |
|
3 |
2 |
4.88 |
61.4 |
-61.4 |
|
3 |
1.26 |
9.20 |
173.6 |
0 |
|
MSC%4 |
3 |
1.37 |
7.20 |
113.1 |
0 |
3 |
1.88 |
5.77 |
60 |
-30 |
|
3/4 |
2.05 |
10.25 |
BB |
BM |
1: Parameter CV = 20%
2: For lw >> lc the Crank Rod profile equals the sine profile, for lw > lc performance deteriorates.
3: Parameter CV = 20%, CA = 20%
4: Parameter n = 30%, alpha = 10%
5: Parameter BB = 30%, BM = 10%
Here j(0) is the initial jerk yerk (derivative of acceleration) and j(1/2) the crossover (halftime) jerk.