Junctions couple one or more elements of a model in a power continuous mode: no energy is stored or dissipated. Examples are a series junction or parallel junction in an electrical network, a fixed connection between two mechanical parts etc. Two types of junctions exist: 0 junctions and 1 junctions.
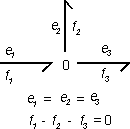
The 0 junction represents a coupling where all efforts of the connected bonds are equal. As a consequence of the property of power continuity the sum of the flows must be equal to zero. The orientation of the bonds determines the sign of the flow summation: all flows of the bonds pointing towards the 0 junction should be added and all flows of the bonds pointing from the 0 junction should be subtracted. This summation corresponds to the Kirchhoff current law for electrical networks. The equality of the efforts, limits the causality. Only one bond may have an "effort-in" causality (the stroke pointed towards the 0 junction). All other bonds must have (seen from the 0 junction) an "effort-out" causality (stroke pointing from the 0 junction). In other words: the 1 junction has a constraint causality.
The 1 junction is the dual form of the 0 junction (effort and flow are opposite). The 1 junction represents coupling where all flows of the connected bonds are equal. As a consequence of the property of power continuity the sum of the efforts must be equal to zero. The orientation of the bonds determines the sign of the flow summation: all efforts of the bonds pointing towards the 1 junction should be added and all efforts of the bonds pointing from the 1 junction should be subtracted. This summation corresponds to the Kirchhoff voltage law for electrical networks. The equality of the flows, limits the causality. Only one bond may have an "effort-out" causality (the stroke pointing from the 1 junction). All other bonds must have (seen from the 1 junction) an "effort-in" causality (stroke pointing to the 1 junction). In other words: the 1 junction has a constrained causality.




