An important aspect in mechatronic systems is the dynamic behavior, i.e. the behavior of the system as function of time. Especially in systems that display swift changes or systems that should behave accurately, the dynamic behavior is important. It is therefore useful to predict the dynamic behavior of a system. Modeling and simulation is useful for making such predictions.
There are various methods of modeling and simulating dynamic systems. A well known one is the Lumped Parameter Method.
With the Lumped Parameter Method, the dynamic behavior of a system is concentrated in discrete points. The interaction of these points gives us insight in the behavior of the real system. The more discrete points are used the more accurate the model will be.
There are various ways to represent lumped parameter models. Well known representations are iconic diagrams, differential equations, block diagrams and bond graphs.
Let's consider the suspension of a car. A lumped parameter model starts with the identification of the various lumps (or parts or components) of this system. We start with the car body. It is supposed to be a rigid body and therefore this part is represented with the icon of a mass. The suspension of the car is represented by a spring damper combination. The wheel is considered to have a significant mass and to be elastic. This component is therefore represented by a mass and spring icon. Finally the road is modeled by path generator function. The resulting ideal physical model (IPM) is shown below.
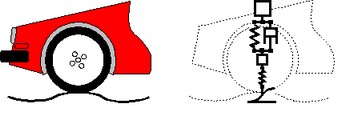
Iconic diagram of a car suspension.



