The 2DSmallRotation library contains models that describe 2-D planar motion and are valid for small rotations. Due to these small rotations, the dynamic equations that describe the various models are simple and can be linearized symbolically. The library is therefore suited for modeling mechanical systems that experience small rotations and must be thoroughly analyzed in the frequency domain.
Consider the guidance system below. Due to the limited stiffness of the guidance wheels, the central body will experience a small rotation that results in a movement in the x-direction at the end-effector. To properly model the end-effector movement as a function of the driven force, this rotation has to be incorporated. To inspect the resulting resonance frequencies in a bode plot, the model must be linearized. If linearization is performed symbolically, the effect of parameter changes (af, b, J) can be inspected directly in the bode plot, which is very useful when the system is still in the design phase.
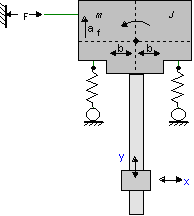
To perform symbolic linearization, the example system should be modeled using the models of the 2DSmallAngles library.
When we speak of 2D motion we often mean all planar motion. However, to describe this motion, three degrees of freedom (displacement x and y and rotation q) are used. In 20-sim we keep to the common naming standard of 2D for planar motion (3 degrees of freedom) and 3D for spatial motion (6 degrees of freedom). In 20-sim the three degrees of freedom for planar motion are combined in a vector notation:
d.o.f. |
identity |
forces |
velocities |
x |
position |
P.F[1] [N] |
P.v[1] [m/s] |
y |
position |
P.F[2] [N] |
P.v[2] [m/s] |
q |
angle |
P.F[3] [Nm] |
P.v[3] [rad/s] |
It is not possible in 20-sim to use vector elements with mixed units. Therefore element number 3 will be displayed with units [m/s] and [N] although it really is [rad/s] and [Nm]!



