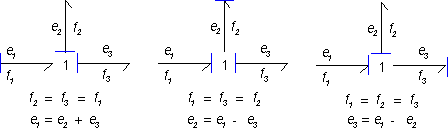Suppose we have the following 1 junction with one bond (1) pointing towards the junction and two bonds (2 and 3) pointing from the junction.

| 1. | For a 1 junction the flows are always equal! This means: |
f1 = f2 = f3
| 2. | The junction is power continuous. For the figure above this means: |
e1×f1 = e2×f2 + e2×f2
| 3. | Combining 1 and 2 yields: |
e1 - e2 - e3 = 0
The last equation can also be derived with the rule of thumb: All effort of the bonds pointing towards a 1 junction should be added and all efforts of the bonds pointing from the 1 junction should be subtracted.
The first equation, limits the causality. Only one bond may have an flow-in causality (the stroke pointed from the 1 junction). All other bonds must have (seen from the 1 junction) a flow-out causality (strokes pointed towards the 1 junction). For the example junction this means three possible causal forms can exist: