Library

Iconic Diagrams\Hydraulics\Restrictions

Use

Domains: Continuous. Size: 1-D. Kind: Iconic Diagrams (Hydraulics).

Description

This model describes the laminar/turbulent flow through an orifice if no cavitation occurs. The flow depends on the pressure difference:

dp = pa.p - pb.p

phi = sign(dp) * Cd * A * sqrt( (2/rho) * abs(dp) ) + GLeak * dp;

Here Cd the discharge coefficient, A the orifice area, rho the fluid density, GLeak the conductance of laminar flow and dp the pressure difference. The discharge coefficient depends on the shape of the orifice and is generally not listed in data sheets. Therefore we will write the turbulent flow with nominal parameters. Given a nominal pressure drop p_nom we find a nominal flow:

Q_nom = Cd * A * sqrt( (2/ rho) * p_nom)

we can use this to rewrite the flow equation as:

phi = Q_nom * sqrt( dp / p_nom)

Similar we can write the laminar leakage flow as

Q_leak = G * p_nom

we can use this to rewrite the complete orifice equation as:

phi = Q_nom * sqrt( dp / p_nom) + (Q_leak/p_nom)*dp

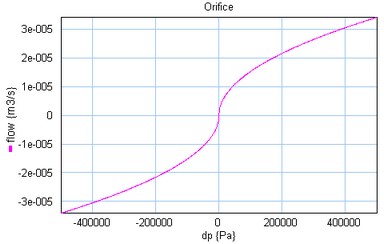
The pressure at both ports has a lower limit that is equal to the vapour pressure. Therefore the actual equations used in this component are:

p1_lim = if pa.p < p_vapour then p_vapour else pa.p end;

p2_lim = if pb.p < p_vapour then p_vapour else pb.p end;

dp = p1_lim - p2_lim;

Interface