Library

Iconic Diagrams\Mechanical\Rotation\Gears

Iconic Diagrams\Mechanical\Translation\Transmission

Use

Domains: Continuous. Size: 1-D. Kind: Iconic Diagrams (Rotation).

Introduction

This models represents a spindle and nut. It transfers an angular motion of the spindle into a translational motion of the nut. The model is ideal, i.e., it does not have inertia or friction. The causality of this model is always mixed: one port has a torque out causality while the other has an angular velocity out causality:

p_spindle.T = i * p_nut.F

p_nut.v = i * p_spindle.omega

or:

p_nut.F = 1/i * p_spindle.T

p_spindle.omega = 1/i * p_nut.v

The model has two implementations which calculate the transform ratio i out of different parameters.

Description - Pitch

In this implementation the transform ratio is calculated using the pitch (the advance of the nut during one revolution of the spindle):

i = pitch / (2 * pi);

Interface - Pitch

Description - LeadAngle

This implementation calculates the transform ratio out of the lead angle alpha and the radius r_spindle of the spindle:

i = tan(alpha)*r_spindle;

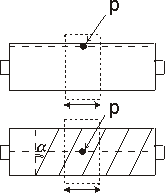
The pitch angle is shown in the figure below. r_spindle is the effective radius of the spindle, i.e. the radius from the center of the spindle to the pitch point p.

Interface -LeadAngle