In the Simulator, select the Tools menu and then click the Linearize Model to start linearization. Linearization will generate a linear, state-space description (linear system) out of any 20-sim model:
dx/dt = Ax + Bu
y = Cx + Du
x(0)
Where:
x = state vector
x(0) = state vector initial value
dx/dt = state vector derivative
y = output
u = input
And:
A = system matrix
B = input gain matrix
C = output gain matrix
D = direct link gain matrix
This linear system shows an input-output behavior that is closely related to the input-output behavior of the original model.
The result is shown in the Linear System Editor. In the Linear System Editor you can choose out of several plot options to show the response of the linear system, such as step responses and Bode plots.
Non-linear models can show variable behaviour. Think for example of an arm. When you stretch it and push against a wall, it is very stiff. When your arm is bent and you push it against a wall, it will be more compliant. Depending on which state it is in, linearization of a non-linear system will therefore result in different linear systems.
To get the correct linear system, we have to bring the non-linear system into the correct state. This can be done by giving it the proper inputs and simulate the system for a while until the desired state is reached. This is called the working point. When the working point is reached, the simulation must be stopped to perform linearization.
When linearization is performed without simulation, the working point is the initial state of the non-linear system.
In the 20-sim Simulator, out of an existing (non-linear) model, a symbolic linear-system can be derived. This means that states, rates and matrix elements are related to the parameters of the original model:
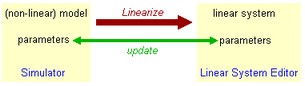
As a result you will get a linear system with the original model parameters that can be changed at will, without having to linearize again.
Symbolic linearization is not possible if the original model contains functions that cannot be differentiated. For such models linearization has to be performed numerically. The resulting linear system has to be recalculated through linearization for different model parameters.
| 1. | Run a simulation until the working point is reached. |
| 2. | Stop the simulation at operating point an select the Linearize command from the Tools menu. |
| 3. | Enter your options in the Linearization Dialog. |
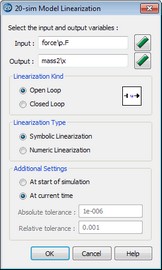
The Linearization Toolbox.
| • | Input: Use the |
| • | Output: Use the |
| • | Linearization Kind: Choose between open loop and closed loop linearization. |
| • | Linearize Type: Choose between Symbolic and Numeric linearization. |
| • | Additional Settings: When you are performing numeric linearization, select At current time when you want to linearize at the operating point where the simulation was stopped. Select At start of simulation when you want to linearize at the start of the simulation. |
| • | Tolerances: 20-sim calculates a numerical linear state space model by small deviations of the complete model from the chosen setpoint. The deviations are based on the given absolute and relative tolerances. For most models the default values are sufficient. For stiff models you can change these values by hand. |
| • | OK: click the OK button to start Linearization. |