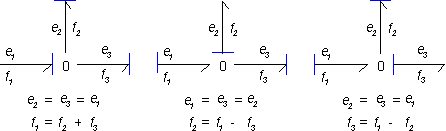Suppose we have the following 0 junction with one bond (1) pointing towards the junction and two bonds (2 and 3) pointing from the junction.
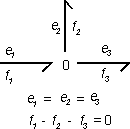
| 1. | For a 0 junction the efforts are always equal! This means: |
e1 = e2 = e3
| 2. | The junction is power continuous. For the figure above this means: |
e1×f1 = e2×f2 + e2×f2
| 3. | Combining 1 and 2 yields: |
f1 - f2 - f3 = 0
The last equation can also be derived with a rule of thumb: All flows of the bonds pointing towards the 0 junction should be added and all flows of the bonds pointing from the 0 junction should be subtracted.
The first equation, limits the causality. Only one bond may have an effort-in causality (the stroke pointed towards the 0 junction). All other bonds must have (seen from the 0 junction) an effort-out causality (strokes pointing from the 0 junction). For the example junction this means three possible causal forms can exist: