Iconic Diagrams\Hydraulics\Valves
Domains: Continuous. Size: 1-D. Kind: Iconic Diagrams (Hydraulics).
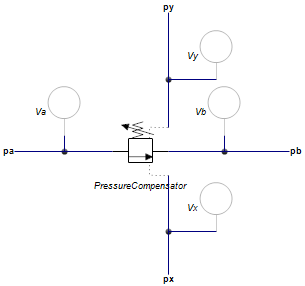
This model is a pressure compensator with parasitic volumes. A pressure compensator is an component that maintains a constant differential pressure across it sensing ports px and py by regulating the flow through the component from port pa to port pb. A pressure compensator can be used to maintain a constant flow over a valve by keeping the pressure drop over the valve constant. The sensing ports py and px are then connected with the input and output of the valve.
The flow through the element is laminar or turbulent depending on the pressure drop p_ab over pa and pb:
p_ab = pa.p - pb.p;
phi = sign(p_ab) * Cd * A * sqrt( (2/rho) * abs(dp) ) + GLeak * p_ab;
The opening A depends on the pressure drop p_xy over pa and pb:

The maximum opening A_max is determined by the maximum flow phi_max at the maximum pressure drop p_in_max over the component:
A_max = phi_max / ( Cd * sqrt( (2/rho) * p_in_max ) );
The opening is at its maximum value when the differential pressure across it sensing ports px and py is below the pressure ((k-1)/k)*p_set. If the differential pressure across it sensing ports px and py is too high, the opening is closed. In between it varies between fully open and fully closed. The speed of response of the components is determined by the proportional gain k (typical choose k = 2 to 5). The proportional gain determines the slope of the valve opening. If k is large the regulator will respond quickly but also induce oscillations in the circuit.
The valve is implemented with second order spool dynamics. I.e. the spool opening is characterized by the bandwidth (f) and damping (d).
Ports |
Description |
pa, pb px, py |
Input and output terminals of the component. Sensing terminals of the component. These are used to measure the pressure and have almost zero flow. |
Causality |
|
preferred pressure out pa preferred pressure out pb preferred pressure out px preferred pressure out py |
|
Parameters |
|
|
PressureCompensator\GLeak PressureCompensator\p_set PressureCompensator\p_in_max PressureCompensator\phi_max
Va\V Va\p_initial Vb\V Vb\p_initial Vy\V Vy\p_initial
|
Mass density of the fluid [kg/m3]. Conductance of the laminar leakage flows [m3/s.Pa], GLeak >= 0. Discharge coefficient [], Cd > 0. Desired differential pressure over xy (px.p - py.p), [Pa]. maximum inlet pressure, [Pa]. maximum flow at maximum inlet pressure (pa.p) and zero outlet pressure (pb.p), [m3/s]. natural frequency of the second order spool dynamics [Hz]. proportional gain [-]. Volume of oil under pressure [m3], (hidden). The starting pressure of the volume [Pa], (hidden). Volume of oil under pressure [m3], (hidden). The starting pressure of the volume [Pa], (hidden). Volume of oil under pressure [m3], (hidden). The starting pressure of the volume [Pa], (hidden). |



