Multi-Dimensional models are models that have connections which are of a size [n,m] with either n or m larger than one. Here n is the numbers of rows and m is the numbers of columns. More information on this matrix notation can be found in the topic on matrices and vectors.
The advantage of multidimensional models is shown in the example below. On top two submodels are connected by three (single) signals. The same submodels are also shown below, connected by one multi-dimensional signal of size [3,1]. If these submodels have to be used a lot, multi-dimensional signals or multi-signals, are easier to use. Multi-dimensional signals, bonds and connections are shown in 20-sim by double lines.

The Secret: Multi-Dimensional Ports
The secret of multi-dimensional models is hidden in the model interface. If you open the Interface Editor to inspect an interface, you will notice that each port (signal, iconic diagram or bond graph) has a default size (dimension) of 1 (1 Row, 1 Column). By increasing the number of rows and/or columns this size can be increased.
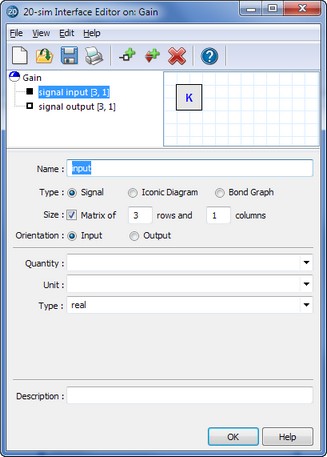
Definition of Multi-ports: increase the number of rows or columns.
The Trick: Automatic Connection
When two submodels are connected, 20-sim will automatically check for the port-sizes and create a connection:
| 1. | If the port-sizes are unequal, an error message will be generated. |
| 2. | If both ports have size one, a single signal, bond or connection will be drawn. |
| 3. | If both ports have a size larger then one, a multi-signal, multi-bond or multi-connection will be drawn. |
The Finishing Touch: Matrices and Vectors
Behind each multi-dimensional submodel, there are equations in the end. To combine multi-dimensional ports with equations, you can use matrices and vectors. 20-sim has a large connection of matrix and vector functions and operators, to help you define any possible matrix equation. For example the gain model in the picture on top, could have been described as shown below.
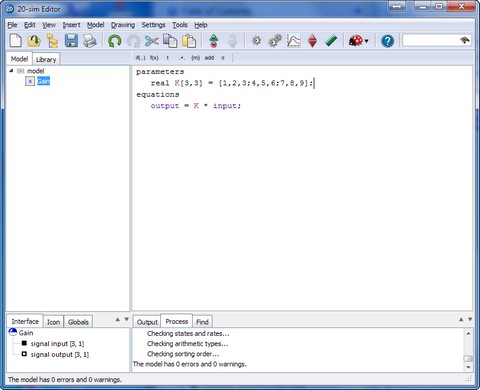
Use the matrix and vector notation to define the model equations.



