This model was named ServoMotor.emx in previous versions of 20-sim!
Iconic Diagrams\Mechanical\Rotation\Actuators
Domains: Continuous. Size: 1-D. Kind: Iconic Diagrams (Rotation).
Industrial servo motors in the medium to high power range generally consist of an AC-electric and drive (the digital controlled current supply of the motor). The drive takes care of the correct supply of current to let the motor follow every desired path. Unfortunately the exact implementation and performance of drives and motors is one of the trade secrets of the commercial motor suppliers. Fortunately modern servo-motors are designed well enough to be described by general parameters that can be found in every data sheet.
The servo motor model describes a digitally controlled AC-motor that is described by general parameters. The model is suited for modeling machine dynamics, i.e. models where the machine behavior is the topic of interest and not the motor itself. For studying the exact motor behavior (temperature, wear, vibration etc.) other motor models should be used. A complete description of the motor is given in the second part of this topic.
Ports |
Description |
p |
Rotation port. |
Causality |
|
preferred angular velocity out p |
|
Inputs |
|
v |
velocity setpoint [rad/s] |
Parameters |
|
VelocityLimit\v_max AccelerationLimit\a_max AccelerationLimit\f_e PI\K PI\Ti PI\Ta PI\T_max TorqueGain\vd |
Maximum motor speed (>0) [rad/s] Maximum allowed acceleration (>0) [rad/s2] Bandwidth drive (half of the sample frequency, >0) [Hz] Proportional gain [] Integral time constant (>0) [s] Tracking time constant (>0) [s] Maximum motor torque (>0) [Nm] Motor speed where torque gain starts to drop (>0) [rad/s] |
TorqueGain\g0 |
Torque gain at zero motor speed (>0, choose equal to 1 to turn off torque gain drop [] |
MotorDynamics\fc Inertia\J |
Bandwidth drive and motor electronics [Hz] Motor inertia [kg.m2/rad] |
|
|
Variables |
There are some variables that can be of interest when inspecting the servo performance: |
PI\error PositionSensor\phi VelocitySensor\omega Inertia\alpha PowerSensor\T PowerSensor\P
|
The error between setpoint and motor velocity [rad/s]. Motor Angle [rad] Motor Speed [rad/s] Motor Acceleration [rad/s2] Output Torque [Nm]. Output Power [W]. |
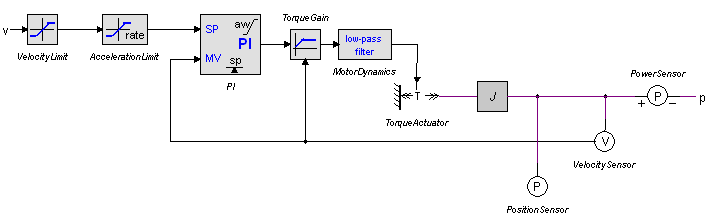
The complete servo motor model is shown below. Every block that is used to form this model will be explained in the next sections. The model has a velocity input signal v and a rotary output port p.
The servo motor model can be used in a machine model as shown in the example below.

Velocity Limit
Most servo motors have a velocity limit to prevent the motor from damage. This limit can be set in the velocity VelocityLimit block. If no limit is known choose twice the nominal velocity.
Acceleration Limit
To prevent the motor from damage, most servos have a maximum acceleration limit. This limit is very important in a model because it can seriously degrade the systems performance.
To find the acceleration, the derivative of the input must be calculated. This is done by means of a first order differentiation with bandwidth f_c. The bandwidth is equal to one half the of the sample frequency of the velocity control loop. Older drives may have loops that run on sample frequencies ranging from 100 Hz to 500 Hz. Modern drives can run the velocity control loop on sample frequencies of 2 kHz or more.
To switch the maximum acceleration limit off, choose the maximum acceleration parameter high enough and choose the bandwidth sufficiently high, preferably 10 times as large as the bandwidth f_e of the motor electronics (specified in the motor dynamics block).
PI-Controller
Most servos will use velocity as the setpoint signal. To calculate the desired torque out of the velocity setpoint, PI-controllers are widely used. For many servos, the controller parameters can be changed by the user, but this is not a very easy task. Therefore these servos often offer automatic tuning facilities.
In 20-sim you can use the Optimization toolbox for automatic tuning. A good starting point is to take the error variable of the PI-controller and minimize it by changing the controller parameters Kp , Ti and Ta. It is important to realize that automatic tuning will tune the controller parameters for a certain task. If you run another task, i.e. perform a simulation with another setpoint, the results may degrade. For varying tasks it is better to use parameters the give a good response over a wide area of loads. To help the user find good starting values, the table below shows some motors, loads and corresponding starting value for the controller parameters.
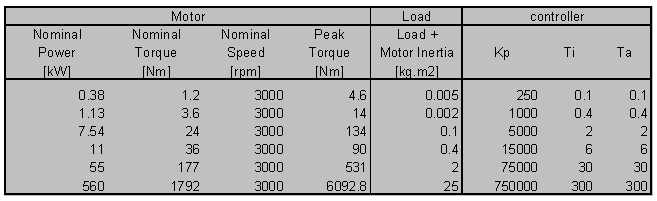
The user has to find the load that should be driven in terms of the rotational inertia. If there is a gear that changes the rotary motion to a linear motion this means the load has to be divided by the square of the gear ratio to get the corresponding load in the rotational domain. Do not forget to add the inertia of the motor itself! For many gear ratios the load in terms of rotational inertia will be of the same magnitude as the motor inertia.
In this model PI-controller with an anti-windup facility is used. This controller is the heart of the servo motor model. It is therefore important to know something about PI-control. More information can be found in the PID controllers section of the library.
AC-motors have a limited output torque which is a complex function of the controller settings, the applied speed, duty cycle, temperature and more. In the servo motor model simply the torque limit of the PI-controller T_max is used which limits the generated torque to a maximum. Because this is a simplification of the real behavior, the maximum torque limit should only be used to inspect what happens to the system when the motor torque is approaching its maximum value. For a proper evaluation of its system, the user should also look at the unconstrained torque. Run a simulation and note the amount of time that the motor runs at a maximum torque. This is called the duty cycle. Every motor manual will have tables showing duty cycles and the corresponding chances of overheating.
Torque Gain
Standard AC-motors, normally designed to run at base speeds between 850 to 3500 rpm, are not particularly well suited for low-speed operation, as their efficiency drops with the reduction in speed. They may also be unable to deliver sufficient smooth torque at low speeds.
An ideal motor will always have a torque gain of 1, i.e. an input signal of 1 Nm will always result in an output torque of 1 Nm. Most industrial motors have a torque gain that is only equal to 1 for higher speeds. At low speeds the torque gain will drop due to electronic limitations. This behavior is represented by the graph below. At speeds below a drop-off speed vd the torque gain drops linearly to a user defined zero speed torque gain g0. If no torque gain drop is desired, choose g0 equal to 1.

Motor Dynamics
The electrical circuits of the drive and wiring of the motor have a limited bandwidth. This is modeled with a first order low-pass filter with a bandwidth f_e. Typical motor bandwidths vary from 3 kHz tot 20 kHz.
Torque source
In the torque source block the torque signal is converted to an iconic diagram port p.
Inertia
This block describes the rotor inertia. The equations of motion of the inertia are used to get the angular acceleration without needing derivatives.
Sensors
Finally four sensors are available to plot the position, velocity, acceleration and output power.
There are some variables in the model that may be of special interest
PI\error PositionSensor\phi VelocitySensor\omega Inertia\alpha PowerSensor\T PowerSensor\P |
The error between setpoint and motor velocity [rad/s]. Motor Angle [rad] Motor Speed [rad/s] Motor Acceleration [rad/s2] Output Torque [Nm]. Output Power [W]. |
All these variables are output signals of their respective blocks. By inserting extra outputs in the servo motor model you can use as output signals for usage in other parts of your model. In the pictures below is shown how to define signals for the torque and power.
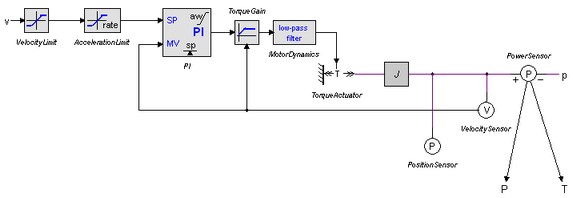
In the servo model define a torque and a power output and connect them.
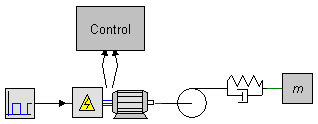
One level higher you can use these signals for modeling, for example in a high level control unit.