Iconic Diagrams\Mechanical\Rotation\Gears
Ideal
Backlash
Domains: Continuous. Size: 1-D. Kind: Iconic Diagrams (Rotation).

This models represents a worm gear with spindle (also referred to as worm) and wheel (also referred to as gear). The gear is ideal, i.e., it does not have inertia or friction. The causality of this model is always mixed: one port has a torque out causality while the other has an angular velocity out causality:
p_spindle.T = i * p_wheel.T
p_wheel.omega = i * p_spindle.omega
or:
p_wheel.T = 1/i * p_spindle.T
p_spindle.omega = 1/i * p_wheel.omega
with
i = tan(alpha)*r_spindle/r_wheel;
Alpha is the pitch angle as shown in the figure below. r_wheel and r_spindle are the effective radii of the wheel and spindle, i.e. the radii from the center of the wheel and spindle to the pitch point p.

Ports |
Description |
p_spindle p_wheel |
Port at the spindle shaft (Rotation). Port at the wheel (Rotation). |
Causality |
|
p_wheel notequal p_spindle |
|
Parameters |
|
r_spindle r_wheel alpha |
pitch radius spindle [m] pitch radius wheel [m] lead angle of the spindle [rad] |

This models represents a worm gear with spindle (also referred to as worm) and wheel (also referred to as gear). Between spindle and wheel, backlash and friction is modelled. The causality of this model is always fixed: both ports have a torque out causality.
The spindle and wheel have one ore more pair of teeth contacting each other. The effective point of contact is called the pitch point P. At the pitch point a frame is defined, with an x- and y-direction. During rotation of the wheel and spindle, the teeth will experience a normal force Fn in the x-direction and a friction force Ff in the y-direction.

Between each pair of teeth, a clearance exists (y-direction), causing backlash. This effect is time-dependent, because of the tooth pairs coming in and out of contact. During normal operation this is a high frequency effect, which is filtered out by the damping of the construction. We therefore only use an average backlash at the pitch point. Using the same reasoning as backlash, an average friction is used at the pitch point.
To define both backlash and friction a frame is used at the pitch point (see picture above) to indicate velocities. The velocity in x-direction is the sliding velocity between the teeth and used to calculate the friction force. The position in y-direction is the position in the clearance and used to calculate the backlash force.
The backlash is described by the standard formula that is also used in the Backlash.emx model. The normal force is modelled by a spring-damper system. Inside the clearance a low damping and stiffness is used (k1 and d1), while a high stiffness and damping (k2 and d2) is used at both ends of the clearance. This yields a normal force Fn of:
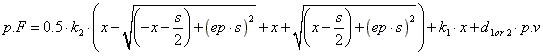
Friction is described as static plus coulomb plus viscous plus Stribeck friction:
p.F = Fn *
(( mu_c + (mu_st*abs(tanh( slope*p.v )) - mu_c)
* exp( -((p.v / v_st)^2 )) ) * sign(p.v)
+ mu_v * p.v);
with:
Fn: the normal force (given by the backlash formula)
mu_s: the static friction coefficient
mu_v: the viscous friction coefficient
mu_c: the coulomb friction coefficient
slope: the steepness of the coulomb and static friction curve.
v_st: the characteristic Stribeck velocity.
A worm gear is said to be self-locking, or irreversible when the wheel cannot drive the spindle. This condition is obtained, if the lead angle of the worm is small and the friction force between the teeth is high enough. Then the friction force becomes larger than the driving force on the teeth. Suppose we only consider static and Coulomb friction and both friction coefficients are equal. Then self locking is obtained when the following condition holds:
mu_s > tan(alpha)
mu_c > tan(alpha)
Ports |
Description |
p_spindle p_wheel |
Port at the spindle shaft (Rotation). Port at the wheel (Rotation). |
Causality |
|
fixed torque out p_spindle |
|
Parameters |
|
r_spindle r_wheel alpha |
pitch radius spindle [m] pitch radius wheel [m] lead angle of the spindle [rad] |
s k1 k2 d1 d2 ep |
Interval of the play [m] Stiffness in the play [N/m] Stiffness outside the play [N/m] Damping inside the play [Ns/m] Damping outside the play [Ns/m] Relative round off (1e-6 -> sharp edges, 1e-2 -> smoother) |
mu_s mu_v mu_c slope v_st |
Static friction coefficient [] Viscous friction coefficient [s/m] Coulomb friction coefficient [] Steepness of Coulomb friction curve [s/m] Characteristic Stribeck velocity [m/s] |
Interesting Variables |
|
Fn Ff v_x v_y x_x x_y |
Average normal force between teeth [N] Average friction force between teeth [N] Velocity in x-direction at the pitch frame [m/s] (used in friction formula) Velocity in y-direction at the pitch frame [m/s] (used in backlash formula) Position in x-direction at the pitch frame [m/s] (used in friction formula) Position in y-direction at the pitch frame [m/s] (used in backlash formula) |