Navigation:  Library > Iconic Diagrams > Mechanical > Rotation > Components > brake

Library

Iconic Diagrams\Mechanical\Rotation\Components

Implementations

C

V

CV

SCVS

LuGre

Use

Domains: Continuous. Size: 1-D. Kind: Iconic Diagrams (Rotation).

Introduction

The brake models represent a disk brake or other type of brake where a rotation is stopped by applying a friction force. The amount of friction depends on the normal force that is applied and the friction function that is used. The normal force is given by the input signal Fn. The brake is mounted to the fixed world.

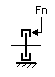
The model has only one initial port p defined. Because any number of connections can be made, successive ports are named p1, p2, p3 etc. 20-sim will automatically create equations such that the resulting torque p.T is equal to the sum of the torques of all connected ports p1 .. pn. The angular velocities of all connected ports are equal to p.omega.

 

p.T = sum(p1.T, p2.T, ....)

p.omega = p1.omega = p2.omega = ....

 

Due to the use of normal force, the brake models all have a fixed torque out causality. The constitutive equations are therefore described as:

 

p.T = Fn * f(p.omega);

 

with f the friction function.

Description - C

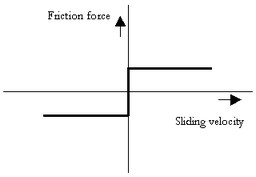
This model represents a brake with braking force described as coulomb friction. The brake is mounted to the fixed world. The amount of friction depends on the normal force that is applied:

 

p.T = Fn*mu_c*tanh(slope*p.omega);

 

Fn: normal force (given by the input signal Fn)

mu_c: the coulomb friction coefficient

slope: the steepness of the coulomb friction curve.

 

 

Interface - C

Description - V

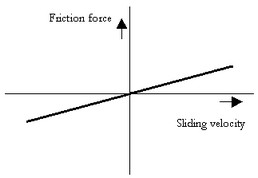
This model represents a brake with braking force described as viscous friction. The brake is mounted to the fixed world. The amount of friction depends on the normal force that is applied:

 

p.T = Fn*mu_v*p.omega;

 

Fn: normal force (given by the input signal Fn)

mu_v: the viscous friction coefficient

 

 

Interface - V

 

Description - CV

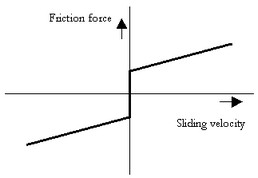
This model represents a brake with braking force described as coulomb plus viscous friction. The brake is mounted to the fixed world. The amount of friction depends on the normal force that is applied:

 

p.T = Fn*(mu_c*tanh(slope*p.omega) + mu_v*p.omega);

 

Fn: normal force (given by the input signal Fn)

mu_v: the viscous friction coefficient

mu_c: the coulomb friction coefficient

slope: the steepness of the coulomb friction curve.

Interface - CV

Description - SCVS

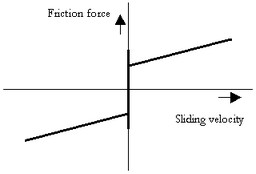
This model represents a brake with braking force described as static plus coulomb plus viscous plus Stribeck friction. The brake is mounted to the fixed world. The amount of friction depends on the normal force that is applied:

 

p.T = Fn *

(( mu_c + (mu_st*abs(tanh( slope*p.omega )) - mu_c)

* exp( -((p.omega / v_st)^2 )) ) * sign(p.omega)

+ mu_v * p.omega);

 

Fn: normal force (given by the input signal Fn)

mu_s: the static friction coefficient

mu_v: the viscous friction coefficient

mu_c: the coulomb friction coefficient

slope: the steepness of the coulomb and static friction curve.

v_st: the characteristic Stribeck velocity.

 

 

Interface - SCVS

Description - LuGre

This model represents a brake with braking force described by the LuGre friction model. The brake is mounted to the fixed world. The amount of friction depends on the normal force that is applied:

 

p.T = FN*f_lg(p.omega);

 

Fn: normal force (given by the input signal Fn)

f_lg: the LuGre friction model

Interface - LuGre