Library

Iconic Diagrams\Mechanical\Translation\2DSmallAngles

Use

Domains: Continuous. Size: 2-D. Kind: Iconic Diagrams (2D Planar).

Description

The central model in the 2DSmallRotation library is the TwoDBody model. It describes a body with three degrees of freedom: x, y and q. The TwoDBody is a point mass with rotational inertia. The constitutive equations are therefore very simple:

P.v = I .* int(P.F);

With

I = [1/M; 1/M; 1/J];

Any number of connections can be made to the TwoDBody model. All forces acting upon the body are added.

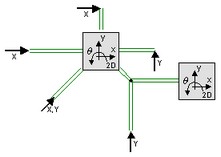
Because any number of connections can be made, successive ports are named P1, P2, P3 etc. 20-sim will automatically create equations such that the resulting force P.F is equal to the sum of the forces of all connected ports P1 . Pn. The velocities of all connected ports are equal to P.v. The model has a preferred velocity out causality. The corresponding constitutive equations then contain an integration. The model can also have the non-preferred force out causality. The constitutive equations then contain a differentiation.

P.F = sum(P1.F, P2.F, ....)

P.v = P1.v = P2.v = ....

velocity out causality (preferred):

I = [1/M;1/M;1/J]

P.v = I*int(P.F);

force out causality:

I = [1/M;1/M;1/J]

P.F = I-1*ddt(P.v);

Interface

Note