Iconic Diagrams\Mechanical\Translation\2DSmallAngles
Domains: Continuous. Size: 1-D/2-D. Kind: Iconic Diagrams (1D Translation, 1D Rotation, 2D Planar).
This model is used to find the absolute acceleration of a TwoDBody model. It has a port P which can be connected to the body and it has three output signals that denotes the x- and y-acceleration and the angular acceleration of the body.
The acceleration output is calculated out of the velocity by differentiation. Differentiation is performed by a state variable filter:
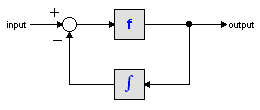
The S-domain function of this filter is equal to:
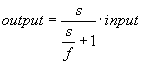
where f is the cut-off frequency. For very high values of f, the output becomes the pure derivative of the input. High values of f, however, increase simulations times. A good trade-off is a starting value of 1e5.
The equations of this model are:
P.F = 0;
ax = 2*pi*f*( P.v[1] - int(ax, 0));
ay = 2*pi*f*( P.v[2] - int(ay, 0));
alpha = 2*pi*f*( P.v[3] - int(alpha, 0));
Ports |
Description |
P[3] |
Port with three degrees of freedom (x, y, q). |
Causality |
|
fixed force out P |
|
Outputs |
|
ax |
Absolute acceleration [m]. |
ay |
Absolute acceleration [m]. |
alpha |
Absolute acceleration [rad]. |
Initial Values |
|
ax_initial |
Initial acceleration [m] |
ay_initial |
Initial acceleration [m] |
alpha_initial |
Initial angular acceleration [m] |



